6.1 Punktereignisse und ihre Transformation
In diesem Modul wird untersucht, welches Ergebnis die Lorentztransformation bei der Transformation eines Punktereignisses liefert. Zwei verschiedene Punktereignisse werden betrachtet und die Relativität der Gleichzeitigkeit wird algebraisch bewiesen.
Hintergrundinformation
In den folgenden Ausführungen wird statt k das in der Literatur übliche gamma verwendet, was nur für einen höheren Leistungslevel zu empfehlen ist.
Lernvoraussetzungen
Die Schülerinnen und Schüler sind mit den folgenden Inhalten vertraut: Ein Punktereignis wird im Bezugssystem S durch die Koordinaten (x, t), genauer (x, y, z, t), und im System S' durch die Koordinaten (x', t'), genauer (x', y', z', t'), beschrieben. Stimmen die Ursprünge der beiden Systeme S und S' zur Zeit t = t' = 0 überein, dann ist die Beziehung zwischen (x, t) und (x', t') durch die Lorentztransformation gegeben:
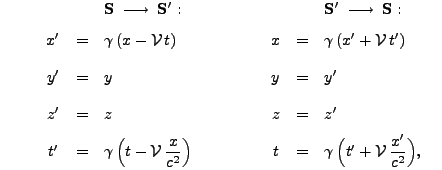
wobei
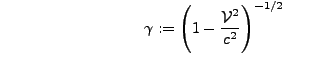
Problemfrage 6.1
Welches Ergebnis liefert die Lorentztransformation bei Transformation eines (Punkt-)Ereignisses (x, t)?
Anregungen für den Unterricht
Es werden zwei verschiedene Punktereignisse betrachtet. Benötigt werden nur die Ergebnisse für
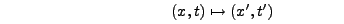
Ereignis 1:

Ereignis 2:

Anschließend wird der räumliche und zeitliche Abstand der Ereignisse im System S' berechnet:
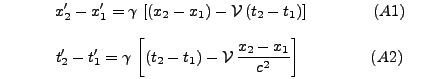
Algebraisch ist damit auch die Relativität der Gleichzeitigkeit bewiesen: Für jeden Beobachter ist Gleichzeitigkeit eine Funktion des verwendeten Bezugssystems. Ein Verständnis für die Implikationen aus den Gleichungen (A1) und (A2) kann erst nach weiterer eingehender Diskussion erzielt werden. Dies soll in den beiden folgenden Modulen geschehen.
Weiterlesen
- 6.2 Zeitdilatation
Aufbauend auf Modul 6.1 betrachten die Schülerinnen und Schüler das Ablesen einer in einem System ruhenden Uhr zu unterschiedlichen Zeiten.





