Vom Lotto zum Pascalschen Dreieck: Unterrichtsverlauf
Das Arbeitsblatt zur Unterrichtseinheit "Vom Lotto zum Pascalschen Dreieck" gliedert sich in zwei Teile, wobei die Lernenden eine zunächst intuitiv beantwortete Frage mathematisch begründen sollen.
Vorgehen
Voraussetzungen und Einstieg
Die Aufgabenstellung gliedert sich in zwei Teile, deren erster ("Konkrete Beantwortung der Fragestellung") die Schülerinnen und Schüler vom Lehrplan der 12. Jahrgangsstufe am Gymnasium abholt. Zum Einstieg und zur Motivation der Fragestellung können eventuell geeignete Zeitungsartikel genutzt werden (siehe Zusatzmaterialien, die einen Bezug zur Realität herstellen. Die schrittweise Modellierung des Problems in den Teilaufgaben 1.1 bis 1.6 gelingt unter der Voraussetzung, dass das "Ziehen mit Zurücklegen" und das "Ziehen ohne Zurücklegen", also die hypergeometrische und die Binomial-Verteilung, bereits bekannt sind.Variation und Verallgemeinerung
Durch die Einführung der Regel von l'Hospital erschließt sich das mathematische Modell den bekannten Mechanismen einer Kurvendiskussion. Außerdem ermöglicht die "ungewohnte" Betrachtung des Binomialkoeffizienten als einer Funktion in n das Anknüpfen an vertraute Sachverhalte. Zu den Themen "Rekursion", "Pascalsches Dreieck" und "Dreieckszahlen" in den Teilaufgaben 2.6 bis 2.9 sollen die Schülerinnen und Schüler selbstständig im Internet oder in entsprechender Literatur nach Hintergründen und Bedeutung recherchieren. Zur Förderung des Verständnisses und zum Abschluss des Modellierungsprozesses wird zu den Ergebnissen der Teilaufgaben generell eine Interpretation beziehungsweise eine Versprachlichung eingefordert.
Arbeitsblatt, Teil 1
Die Lernenden werden mit folgender Fragestellung konfrontiert: "Ist es wahrscheinlicher, dass es bei der ("6 aus 49"-) Lotterie mehr Jackpot-Gewinnerinnen und -gewinner gibt, wenn es mehr Teilnehmende gibt?" Diese Fragestellung soll diskutiert und zunächst intuitiv beantwortet werden. In der Regel wird sich schnell ein Konsens einstellen: Ja. Doch wie genau bleibt noch offen und zu untersuchen. Nach der Ermittlung der Trefferwahrscheinlichkeit für "r Richtige plus Zusatzzahl" sowie der Wahrscheinlichkeit dafür, dass k von insgesamt n Lotterie-Teilnehmerinnen und-teilnehmer r Richtige getippt haben, stellt sich das mathematische Gesamtmodell als eine Kombination aus hypergeometrischer und binomial-verteilter Formulierung dar. Nach einigen konkreten Berechnungen wird für Grenzwertbetrachtungen zum einen die (mittlerweile im Lehrplan oft nur noch optionale) Regel von l'Hospital und zum anderen die einfache, aber mächtige Identität
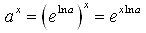
für a > 0 eingeführt. Damit lassen sich alle Grenzwert- und Monotoniebetrachtungen durchführen. Anhand des Graphen für einen geeigneten Spezialfall werden die Schülerinnen und Schüler zur abschließenden Beantwortung der Ausgangsfrage geführt.
Weiterlesen
- Variation und Verallgemeinerung
Der zweite Teil verallgemeinert die Fragestellung des ersten Teils und führt zu tiefer liegenden mathematischen Sachverhalten.




