2. und 3. Stunde: Ursprungsgeraden, deren Steigung und Gleichung
Während die erste Unterrichtsstunde konkret anschaulich angelegt war, folgt nun eine schrittweise Abstraktion bis hin zur Bestimmung der Gleichung einer Ursprungsgeraden aus den Koordinaten eines gegebenen Punktes ohne veranschaulichende Zeichnung.
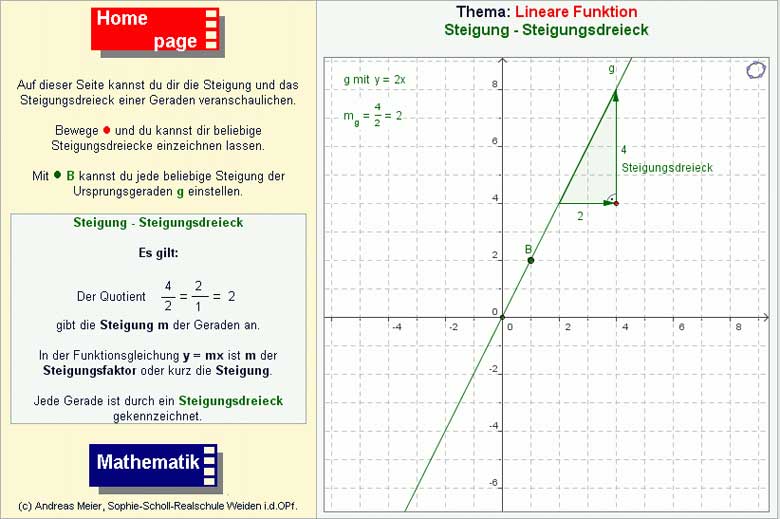
Steigung und Steigungsdreieck
Das dritte Online-Arbeitsblatt (Abb. 3, Platzhalter bitte anklicken) dient zur Veranschaulichung der Steigungsdreiecke von Ursprungsgeraden. Durch die Bewegung von Punkten können die Schülerinnen und Schüler verschiedene Steigungsdreiecke und Ursprungsgeraden einstellen. Aus der dynamischen Darstellung lässt sich so ablesen, dass der Quotient
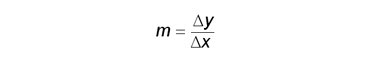
stets konstant ist und es für die Berechnung von m Steigungsdreiecke gibt, aus denen der Steigungsfaktor sehr leicht bestimmt werden kann. Bei der Verwendung dieses Arbeitsblatts sind die Lernenden selbst dafür verantwortlich, wie viele unterschiedliche Geraden und Steigungsdreiecke sie zeichnen wollen, um sich den Sachverhalt zu verdeutlichen. Sind sie der Ansicht, den Sachverhalt verstanden zu haben, so können sie sich mit den unterschiedlichen Übungen beschäftigen.
Variables Übungsangebot - Differenzierung und Individualisierung
Der zeitliche Umfang der im Folgenden eingesetzten drei Online-Arbeitsblätter und des Arbeitsblatts (steigung_funktionsgleichung.pdf) richtet sich nach der individuellen Zusammensetzung der Klasse. Zwei Unterrichtsstunden sind in den meisten Fällen realistisch.
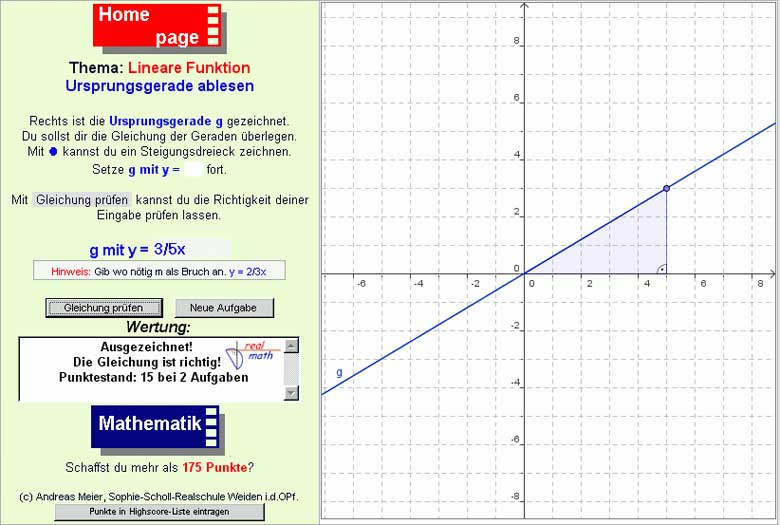
Gleichung einer Ursprungsgeraden angeben
Aus dem Online-Arbeitsblatt 4 (Abb. 4) soll die Lerngruppe die Gleichung einer vorgegebenen Ursprungsgeraden ablesen. Dabei bietet das Arbeitsblatt die Möglichkeit, dass sich die Schülerinnen und Schüler zur Bearbeitung der Aufgabe ein günstiges Steigungsdreieck einzeichnen und so die Gleichung der Ursprungsgeraden bestimmen können. Mit "Gleichung prüfen" wird die Schülereingabe kontrolliert, mit "Neue Aufgabe" werden weitere Aufgaben gestellt. Dabei können leistungsstärkere Klassenmitglieder angehalten werden, die Gleichung der Ursprungsgeraden anzugeben, ohne sich ein Steigungsdreieck zu zeichnen, während andere weiterhin diese Veranschaulichung benutzen.
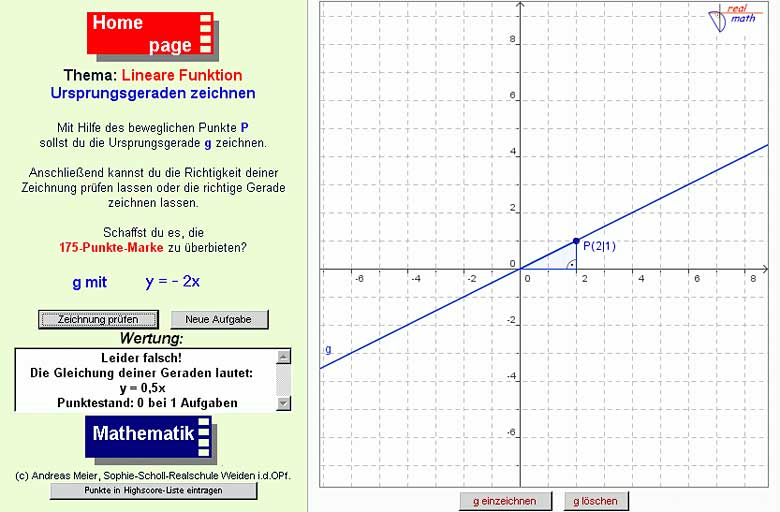
Ursprungsgerade nach vorgegebener Gleichung zeichnen
Mithilfe eines Punktes, dessen Koordinaten in Echtzeit angezeigt werden, soll im Online-Arbeitsblatt 5 (Abb. 5) eine Ursprungsgerade gezeichnet werden, deren Gleichung gegeben ist. Die Schülerinnen und Schüler erhalten stets eine Rückmeldung bezüglich ihrer gezeichneten Geraden und können sich bei Bedarf sogar die Lösung einzeichnen lassen. Deshalb eignet sich dieses Arbeitsblatt sehr gut für einen individualisierten Unterricht. Die Lehrkraft greift nur dann ein, wenn die Lernenden mit den Rückmeldungen nicht zurechtkommen. Die Lehrkraft wird damit zu einem Moderator im Lernprozess. Die Möglichkeit, eigenständig Wissen zu erwerben und auch anwenden zu können, steigert dabei in hohem Maße die Eigenverantwortlichkeit der Schülerinnen und Schüler.
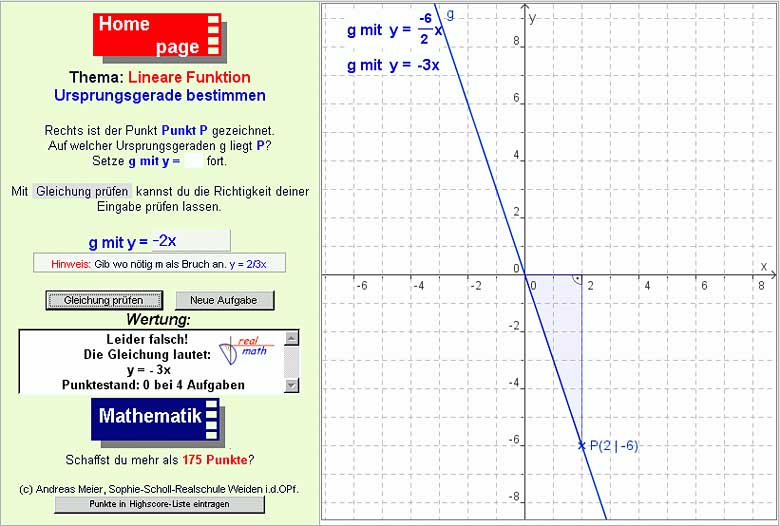
Gleichung der Ursprungsgeraden aus einem Punkt ermitteln
In Online-Arbeitsblatt 6 (Abb. 6) besteht die Aufgabe darin, die Gleichung einer Ursprungsgeraden anzugeben, von der nur die Koordinaten eines Punktes gegeben sind. Zur Veranschaulichung wird dieser Punkt aber noch in ein Koordinatensystem eingezeichnet. Die Schülerinnen und Schüler müssen sich anhand der Lage des Punktes ein Steigungsdreieck vorstellen. Diese Übung leitet damit den Abstraktionsprozess ein, durch den später Gleichungen von Ursprungsgeraden ohne konkrete Zeichnung rechnerisch bestimmt werden sollen. Nach der Eingabe der Gleichung und der Betätigung des Buttons "Gleichung prüfen" werden die Berechnung der Gleichung der Ursprungsgeraden und die Gerade selbst eingeblendet. Dies soll den Lernenden den Bearbeitungsweg und die Lösung der Aufgabe verdeutlichen. Die flexible und informative Rückmeldung eröffnet dabei auch die Möglichkeit einer eigenständigen Fehleranalyse.
Besonderheiten der interaktiven dynamischen Übungsform
Motivation durch Wettbewerbssituation
Die Vergabe von Punkten bei allen Übungen und die damit verbundene Wettbewerbssituation führt zu einer zusätzlichen Motivation. Das so erzeugte spielerische Element innerhalb der mathematischen Übungen ist eines der wesentlichen Merkmale aller zur Lernumgebung gehörenden Aufgaben. Man kann im Unterricht immer wieder beobachten, dass sich Schülerinnen und Schüler bei Wettbewerben in einem Maße engagieren, wie dies im herkömmlichen Unterricht nicht der Fall ist.
Vom Belehren und Korrigieren zur Kooperation - die neue Lehrerrolle
Für jede gelöste Aufgabe gibt es 15 Punkte. Die Anzeige des Punktestandes und der Aufgabenzahl ermöglicht es der beobachtenden Lehrkraft, die jeweiligen Schülerleistungen schnell einzuschätzen. So ist es möglich, Klassenmitglieder gezielt zu loben, aber auch leistungsschwächeren Schülerinnen und Schülern individuell zu helfen. Die Lehrkraft tritt somit aus der belehrenden, korrigierenden Rolle heraus - dies übernimmt der Computer - und übernimmt eine moderierende, unterstützende und kooperative Rolle.Herkömmliche Lernzielkontrolle mit Papier und Bleistift
Abschließend kann eine Leistungserhebung durchgeführt werden (geradensteigung_test.pdf), bei der die Inhalte der vorangegangenen drei Übungen abgefragt und die Leistungen der Schülerinnen und Schüler überprüft werden. Dieser Test kann aber auch als Hausaufgabe gegeben oder in Form einer Partnerarbeit im Anschluss an die Online-Arbeitsblätter bearbeitet werden. So mündet die Arbeit am Computer wieder in die herkömmliche Unterrichtsarbeit im Klassenzimmer.
Zurück
- Steigung einer Geraden - mit GeoGebra entwickeln
Über diesen Link gelangen Sie zurück zur Startseite der Unterrichtseinheit "Steigung einer Geraden - mit GeoGebra entwickeln".