Graphen von Potenzfunktionen: Voraussetzungen und Hinweise zu den Materialien

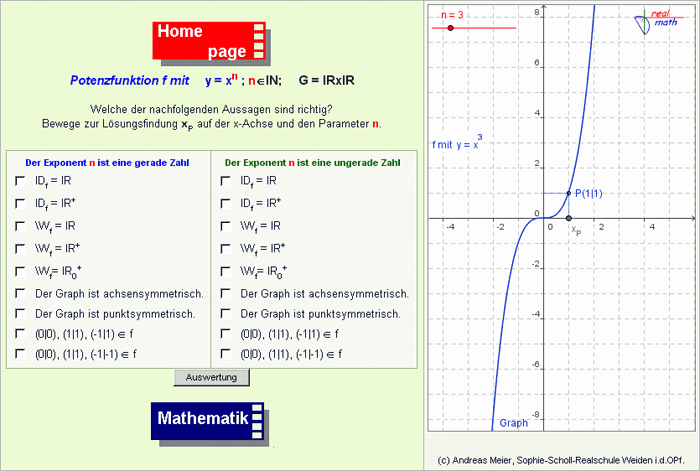
Die Bedienung aller Online-Arbeitsblätter ist identisch und ermöglicht somit nach einer kurzen Einführung durch die Lehrkraft ein selbstständiges Arbeiten der Schülerinnen und Schüler. Bei allen Arbeitsblättern wird beim Seitenstart der dynamische Graph einer Potenzfunktion erzeugt. Die Schülerinnen und Schüler sollen dabei die in der linken Spalte des Arbeitsblatts stehenden 18 Aussagen überprüfen und die zutreffenden jeweils per Mausklick auswählen (Abb. 1, Platzhalter bitte anklicken). Zur Lösungsfindung können sie mit dem Schieberegler n unterschiedliche Funktionsgraphen erzeugen. Wenn die Schülerinnen und Schüler der Ansicht sind, alle Eigenschaften gefunden zu haben, so können sie ihre Lösung mit einem Klick auf den Button "Auswertung" überprüfen lassen.

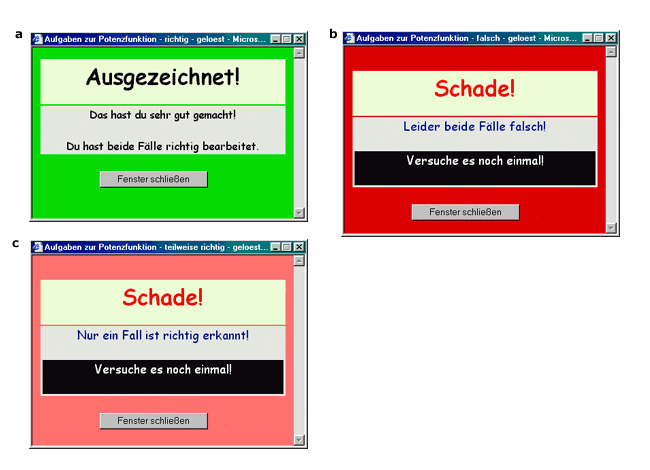
Je nach Richtigkeit und Vollständigkeit der Schülerbeobachtung wird ein entsprechendes Pop-up-Fenster erzeugt. Sind alle Eigenschaften richtig zugeordnet erscheint die Bestätigung: "Ausgezeichnet! Das hast du sehr gut gemacht! Du hast beide Fälle richtig bearbeitet." (Abb. 2a)." Wurde hingegen keiner der beiden Fälle richtig bearbeitet, erscheint im Pop-up-Fenster die Meldung: "Schade! Leider beide Fälle falsch! Versuche es noch einmal!" (Abb. 2b). Hat eine Schülerin oder ein Schüler einen der beiden Fälle, zum Beispiel "n ist gerade", richtig analysiert und den Fall "n ist ungerade" falsch oder unvollständig beschrieben, so erscheint im Pop-up-Fenster die Meldung: "Schade! Nur ein Fall ist richtig erkannt! Versuche es noch einmal!" (Abb. 2c). Bei den Rückmeldungen auf unvollständige oder falsche Eingaben erfolgt keine detaillierte Fehleranalyse. Die Schülerinnen und Schüler werden dadurch gezwungen, alle Aussagen erneut auf ihre Richtigkeit zu überprüfen und ihre Beobachtungen zu präzisieren.