Graphen von Potenzfunktionen: Unterrichtsverlauf
Hinweise zur Nutzung der einzelnen Arbeitsblätter mit Screenshots; die „klassischen“ Materialien können Sie hier einzeln herunterladen.
Funktionen mit der Gleichung y = axn
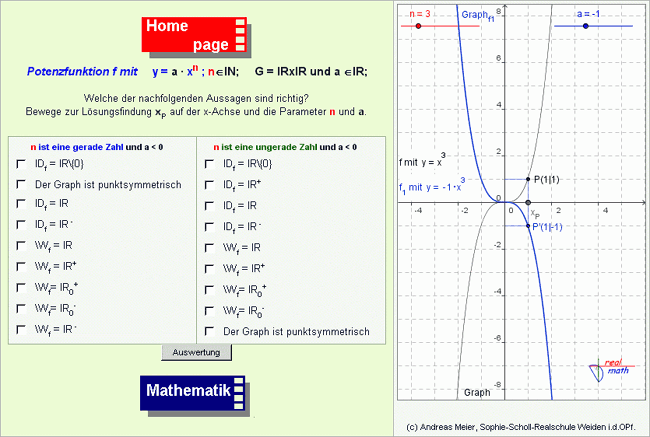
In einem weiteren Schritt schließt sich im Unterricht die Betrachtung von Funktionsgraphen an, denen die Gleichung y = axn zu Grunde liegt. Aufbau und Funktionsweise des Arbeitsblatts (Abb. 3, Platzhalter bitte anklicken) sind identisch zum vorhergehenden. Das dynamische Element besitzt zusätzlich einen Schieberegler für den Parameter a. Neben dem Graphen zur Funktion y = axn wird der Graph zur Funktionsgleichung y = xn dynamisch erzeugt und grau eingezeichnet. Dadurch lassen sich die Veränderungen der Graphen, die durch den Parameter a veranlasst werden, gezielt beobachten. Die Aufgabe der Schülerinnen und Schüler besteht wieder darin, die Eigenschaften der Funktionen zu finden.2. Unterrichtsstunde
Funktionen mit der Gleichung y = x-n
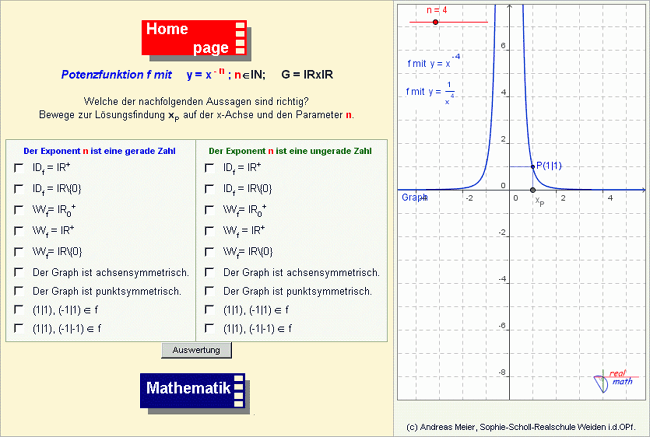
Die Konzeption der zweiten Unterrichtsstunde orientiert sich am Verlauf der vorhergehenden. Nach einer kurzen Zusammenfassung der bisherigen Ergebnisse anhand der dort angefertigten Folie erfolgt eine Einführung in die Funktionsweise des Arbeitsblatts (Abb. 4) durch die Lehrkraft. Die Schülerinnen und Schüler experimentieren dann wieder eigenständig, um die Eigenschaften der vorliegenden Funktionen zu erkunden. Im Anschluss werden die Eigenschaften von Potenzfunktionen mit negativen ganzzahligen Exponenten im Arbeitsblatt "hefteintrag_2.pdf" festgehalten. Die Zuordnung der vier Funktionsgraphen im PDF-Arbeitsblatt kann wieder in Partnerarbeit als Element einer Ergebnissicherung verwendet werden.Funktionen mit der Gleichung y = ax-n
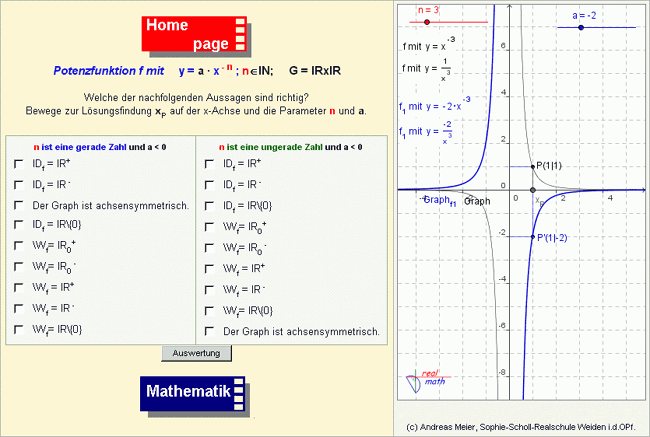
Es schließt sich im weiteren Verlauf der Unterrichtsstunde die Betrachtung von Funktionsgraphen an, denen die Gleichung y = ax-n zu Grunde liegt (Abb. 5). Aufbau und Funktionsweise des Arbeitsblatts sind im Wesentlichen wieder identisch zum vorhergehenden. Zusätzlich besitzt das dynamische Element des Arbeitsblatts einen Schieberegler für den Parameter a. Der Graph zur Funktionsgleichung y = x-n wird ebenfalls wieder erzeugt und grau eingezeichnet. Haben die Schülerinnen und Schüler die Eigenschaften gefunden, können sie erneut ihre Angaben mit einem Klick auf den Button "Auswertung" prüfen lassen.3. Unterrichtsstunde - Übung, Anwendung und Festigung
Graphen werden Funktionsgleichungen zugeordnet
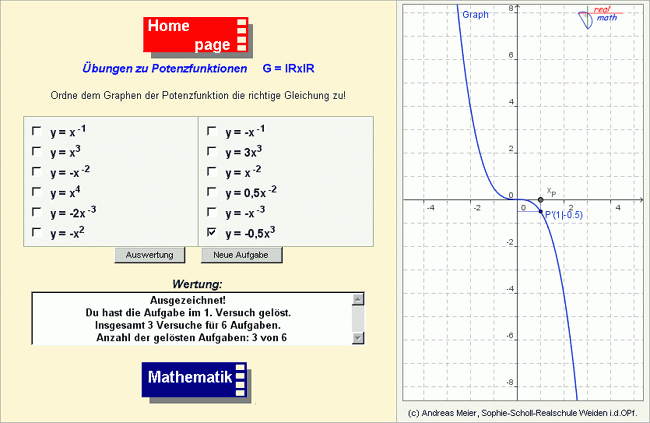
Mit den Übungen der dritten Unterrichtsstunde können die Schülerinnen und Schüler ihre Kenntnisse bezüglich der Eigenschaften von Potenzfunktionen weiter vertiefen und auf unterschiedliche Graphen anwenden. Das dynamische Arbeitsblatt (Abb. 6) weist die gewohnte Zweiteilung auf. In der linken Spalte sind zwölf Funktionsgleichungen vorgegeben. Beim Seitenstart oder nach dem Klick auf den Button "Neue Aufgabe" wird in der rechten Spalte des Arbeitsblatts der Graph einer Potenzfunktion erzeugt. Dabei kann zur Lösungsfindung ein Punkt auf dem jeweiligen Graphen bewegt werden, dessen Koordinaten fortlaufend aktualisiert und angezeigt werden. Die Aufgabe der Schülerinnen und Schüler besteht darin, die richtige Gleichung für den gezeichneten Graphen anzugeben, in dem sie diese per Mausklick aus den gegebenen Gleichungen auswählen. Nach einem Klick auf den Button "Auswertung" erhält die Schülerin oder der Schüler eine der Eingabe entsprechende Rückmeldung.Differenzierte Auskunft über Schülerleistungen
Die Rückmeldung gibt dabei neben der Bewertung der Schülerlösung zusätzlich Auskunft darüber, wie viele Lösungsversuche die Schülerin oder der Schüler für die aktuelle Aufgabe benötigt hat, wie viele Versuche insgesamt unternommen wurden und wie viele Aufgaben bisher gelöst wurden. Die beobachtende Lehrkraft erhält so einen schnellen Überblick über die Leistungsfähigkeit der Schülerinnen und Schüler.Schriftliches Formulieren, um Kenntnisse zu festigen und zu vertiefen
An diese Übung am Computer schließt sich wieder eine Zusammenfassung mit einer herkömmlichen Übung an. Dabei kommt das Arbeitsblatt "potenzfunktionen_quiz.pdf" zum Einsatz. Auch hier sollen Funktionsgraphen Funktionsgleichungen zugeordnet werden. Doch sollten die Schülerinnen und Schüler nun zusätzlich schriftlich festhalten, an welchen Besonderheiten des Graphen sie die Funktionsgleichung bestimmt haben. Das schriftliche Formulieren von gewonnenen Erkenntnissen ist nach einer am Computer durchgeführten Übung immer notwendig, damit sich die Lernenden mit der den Aufgaben zu Grunde liegenden Struktur auseinandersetzen und so ihre Kenntnisse weiter festigen und vertiefen können.
Zurück
- Potenzfunktion - Graphen analysieren, Eigenschaften finden
Über diesen Link gelangen Sie zurück zur Startseite der Unterrichtseinheit "Potenzfunktion - Graphen analysieren, Eigenschaften finden".