Gemischte Zahlen subtrahieren: Erste Unterrichtsstunde
Die Schülerinnen und Schüler führen Übungen zur Subtraktion eines Bruchs von einer natürlichen Zahl und zur Subtraktion eines Bruchs von einer gemischten Zahl durch.
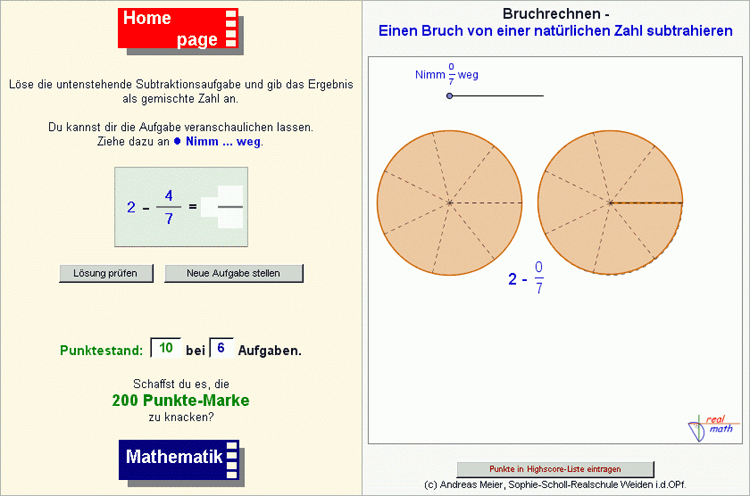
Subtraktion eines Bruchs von einer natürlichen Zahl
Die Einbettung der natürlichen Zahlen in die Bruchzahlen ist eine notwendige Grundlage für das Verständnis von gemischten Zahlen und deren Subtraktion. Um möglichen Fehlvorstellungen bei der Einbettung natürlicher Zahlen in die Bruchzahlen zu begegnen, wird zu Beginn eine visuelle Einbettung der natürlichen Zahlen in die Bruchzahlen vorgenommen. Als Anschauungsmodell zur Visualisierung wird im zugehörigen interaktiven dynamischen Arbeitsblatt (Abb. 1, Platzhalter bitte anklicken) die gleichmäßig unterteilte Kreisfläche verwendet. Diese Darstellung nimmt Bezug zur Alltagserfahrung der Schülerinnen und Schüler. So können die Lernenden zum Beispiel mit der Kreisfläche eine Pizza assoziieren. Die bräunliche Farbgebung der Kreisfläche und die gestrichelte Unterteilung in gleich große Stücke soll diese mögliche Assoziation einer vorgeschnittenen Pizza unterstützen. Die durch das interaktive dynamische Arbeitsblatt ermöglichte intuitive und anschauliche Begegnung mit Aufgaben der Art "1 minus 7/5" oder "3 - 1/3" soll die Schülerinnen und Schüler befähigen, Aufgaben dieses Typs - ohne jeden Rechenkalkül - einfach durch Anschauung zu lösen.
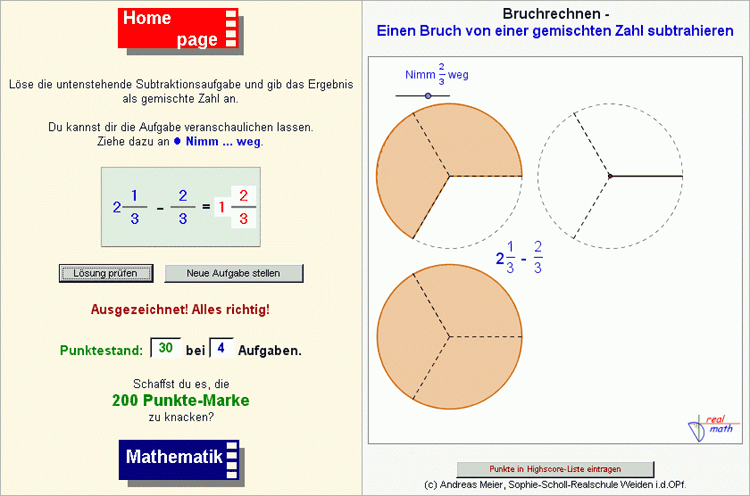
Subtraktion eines Bruchs von einer gemischten Zahl
Bei der Veranschaulichung der Subtraktion eines Bruchs von einer gemischten Zahl stehen zwei Gesichtspunkte im Vordergrund. Zum einen wird die bildliche Darstellung einer gemischten Zahl in Form von ganz gefüllten Kreisen und einem zusätzlichen Kreissegment eingeführt oder aus dem vorangegangenen Unterricht wieder aufgegriffen und zusätzlich die Subtraktion mit und ohne Umwandlung zum ersten Mal problematisiert. Bei der Gestaltung des zweiten interaktiven dynamischen Arbeitsblatts (Abb. 2) wurde auf Kontinuität geachtet, das heißt Aufbau und Funktionsweise entsprechen dem ersten Arbeitsblatt. Die Schülerinnen und Schüler müssen sich daher nicht erst an eine neue Aufgabenumgebung gewöhnen, sondern können sich unmittelbar mit der mathematischen Problemstellung auseinandersetzen. Ein fließender Übergang zur Bearbeitung von Aufgaben zur Subtraktion eines Bruchs von einer gemischten Zahl ist somit gegeben.
Zusammenfassung und Hefteintrag
Nachdem die Schülerinnen und Schüler die ersten beiden interaktiven dynamischen Arbeitsblätter bearbeitet haben, erfolgt eine Zusammenfassung der Ergebnisse im Heft. Beim Hefteintag ist darauf zu achten, dass die Verbindung zur vorherigen Arbeit der Schülerinnen und Schüler hergestellt wird. Hierzu kann das Arbeitsblatt "ab_hefteintag_1.pdf" verwendet werden, bei dem die Lernenden die Subtraktion eines Bruchs von einer natürlichen Zahl und die Subtraktion eines Bruchs von einer gemischten Zahl noch einmal zeichnerisch durchführen müssen. Damit soll einer allzu schnellen und rein symbolischen Lösung der Aufgaben begegnet und den Lernenden Zeit gegeben werden, ihr Vorgehen zu reflektieren.
Anwendung ohne Veranschaulichung als Lernzielkontrolle
Den Abschluss der Unterrichtsstunde kann die Bearbeitung der Aufgaben der interaktiven dynamischen Arbeitsblätter ohne Veranschaulichung bilden. Je nach Klassensituation kann aber auch die Bearbeitung von Aufgaben auf bildlicher Ebene mithilfe des Arbeitsblatts "ab_hausaufgabe_1.pdf" fortgesetzt werden. Zur Erstellung von Hausaufgaben auf bildlicher Ebene kann die Kopiervorlage "bruchteile.pdf" verwendet werden.
Weiterlesen
- Zweite Unterrichtsstunde
Die Lernenden führen Übungen zur Subtraktion einer natürlichen Zahl von einer gemischten Zahl und zur Subtraktion zweier gemischter Zahlen durch
- Dritte Unterrichtsstunde
In der letzten Stunde der Unterrichtseinheit soll der Aspekt der unterrichtlichen Differenzierung im Mittelpunkt stehen.