Unterrichtsverlauf "Sinusfunktion"
Zunächst wird als periodischer Vorgang die Sonnenaufgangskurve untersucht. Rein harmonische Schwingungen werden dann mithilfe des Computers betrachtet.
Einführung
Untersuchung periodischer Vorgänge
Nachdem die Schülerinnen und Schüler mit der Beschreibung der Natur durch Potenzfunktionen bereits mehr oder weniger vertraut sind, sollen als neue Funktionsklasse nicht gleich die Sinusfunktionen, sondern erst einmal beliebige periodische Vorgänge untersucht werden. Direkt am Phänomen können Amplitude und Periodenlänge als wichtigste Begriffe erfahren werden (Experimentvorschläge finden Sie auf den Arbeitsblättern 1 und 2). Dabei erscheint mir das Wort Periodenlänge (und nicht Periodendauer, Periode oder Schwingungsdauer) für die Beschreibung der Periode im Mathematikunterricht als am besten geeignet. Hier legt man sich nicht schon im Voraus auf zeitliche Perioden fest. Der Frequenzbegriff ist vom mathematischen Standpunkt aus erst einmal nicht nötig. Auch auf den Begriff der Winkelgeschwindigkeit verzichte ich, auch wenn seine konsequente Verwendung durchaus denkbar ist. Phasenunterschiede sind für das Phänomen an sich primär nicht von großer Bedeutung und werden deshalb vorerst nicht behandelt. Daher wird auch nur die Sinusfunktion und nicht zusätzlich auch noch die Kosinusfunktion eingeführt.
Die Sonnenaufgangskurve als nichtphysikalisches Sicherungselement
Die Begriffe Amplitude und Periodenlänge sollen erst hinreichend gesichert werden, bevor sich die harmonische Schwingungsfunktion als wichtigste periodische Funktion herauskristallisiert. Dazu eignen sich insbesondere Experimente aus der Akustik. Hier kann man Amplitude und Periodenlänge direkt hören und mit dem Oszilloskop sogar sichtbar machen. Als nichtphysikalische Sicherungselemente bieten sich insbesondere tages- und jahreszeitliche Perioden an. Ich habe mich für die Änderung der Sonnenaufgangszeit im Laufe des Jahres entschieden, weil dieses Problem zum Beispiel im Herbst höchst aktuell und schülernah ist. Die Sonnenaufgangskurve weicht zwar mit zunehmender geographischer Breite von einer Sinuskurve ab, diese Abweichungen betragen in Deutschland jedoch weniger als fünf Prozent.
Untersuchung rein harmonischer Schwingungen
Definition der Funktion
Erst nach der beschriebenen Einführung wird die Kreisbewegung ins Spiel gebracht und es erfolgt eine Beschränkung auf die rein harmonischen Schwingungen. Das klassische Experiment dazu ist die synchrone Projektion von Federpendel und Kreisbewegung eines Stiftes. Vor der Definition von sin(x) sollen die Schülerinnen und Schüler erkennen, dass die harmonische Schwingungsfunktion keine Potenzfunktion sein kann. Das erste Mal in ihrer mathematischen Laufbahn können sie eine funktionale Abhängigkeit nicht aus den bekannten Rechenoperationen zusammenstellen. Eine neue Funktion muss definiert werden. Das hört sich einfacher an, als es ist, denn man bekommt bei einer solchen Definition sehr viele Freiheiten mit auf den Weg. Die Kurvenform ist zwar mehr oder weniger festgelegt, doch stehen die Achsenbeschriftungen noch völlig frei. Um hier zu steuern, werden die Schülerinnen und Schüler vorher in einem Arbeitsblatt die harmonische Schwingungskurve für eine Projektion eines Punktes auf einer Kreisbahn mit festem Radius genau zeichnen (Arbeitsblatt 4). Dadurch liegt es nahe, die neue Funktion im Bogenmaß zu definieren, nur der Radius sollte noch normiert werden. Argumente im Winkelmaß führte ich erst später ein. Um schnell von der Kreisbewegung zum Graphen der Sinusfunktion zu gelangen, bietet sich das Applet von Walter Fendt an (siehe externe Links auf der Startseite dieser Unterrichtseinheit). Wer etwas mehr Zeit hat, kann seine Schülerinnen und Schüler natürlich auch auf die herkömmliche Art und Weise die Projektion des Einheitskreises mithilfe des oben genannten Arbeitsblattes durchführen lassen, diesmal allerdings vor dem Hintergrund einer echten Bewegung.
Kartierung der Funktion
Nach der Definition wird die Funktion zu Hause punktweise kartiert und erst anschließend mit der Taschenrechnertaste "sin" in Verbindung gebracht und als Ganzes möglichst genau gezeichnet. Damit die Schülerinnen und Schüler wirklich das Gefühl einer eigenen Definition haben, soll die Namensgebung sehr offen gestaltet werden. Ein weiterer Vorteil eines vorerst anderen Namens besteht darin, dass die Lernenden bei der Kartierung der Funktion nicht zum "Mogeln" mit dem Taschenrechner gedrängt werden.
Einsatz des Computers
Die "nackte" Sinusfunktion reicht zur Beschreibung der harmonischen Schwingungen noch nicht aus, sie muss verschoben, gestreckt und gestaucht werden. Dabei sollen die Schülerinnen und Schüler lernen, zu vorgegebenen Funktionen der Art f(x) = A sin(B x) + C den zugehörigen Funktionsgraphen skizzieren zu können und umgekehrt zu festen Periodenlängen, Amplituden und Verschiebungen die zugehörige Funktion nennen zu können. Phasenverschiebungen werden aus den genannten Gründen nur kurz behandelt. Bei dieser Vorgehensweise bietet es sich außerdem an, auch die Überlagerung von Schwingungen und damit das Additionstheorem
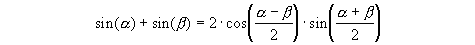
am Phänomen der Schwebung zu erfahren.
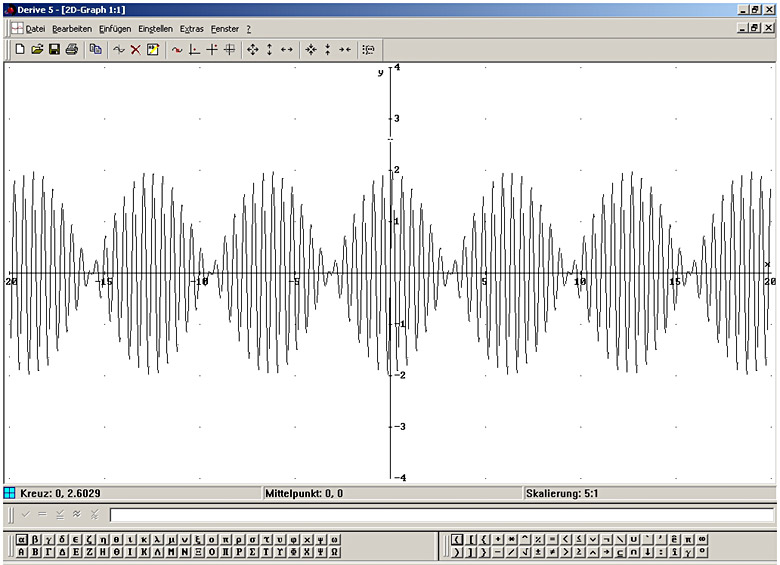
Die Lernenden sollen das Additionstheorem hören (langsame Amplitudenschwankungen bei ähnlicher Frequenz wie die Grundtöne) und dann mithilfe eines CAS, eines Funktionenplotters oder eines geeigneten Java-Applets den Funktionsgraphen ermitteln. Abb. 1 (Platzhalter bitte anklicken) zeigt die Darstellung einer Schwebung mit dem CAS Derive, die durch Addition von sin(12x) und sin(13x) entsteht (verwendbare Online-Materialien wie zum Beispiel Java-Applets finden Sie unter den externen Links auf der Startseite dieser Unterrichtseinheit). Dabei werden die Begriffe Amplitude und Periodenlänge nochmals gesichert und gefestigt.
Weiterlesen
- Bezug der Unterrichtseinheit zu SINUS-Transfer
"Weiterentwicklung der Aufgabenkultur" (Modul 1) und "Fächerübergreifendes Arbeiten" (Modul 6)