Fotografieren, bearbeiten, auswerten
Das mathematische Rüstzeug für die Bestimmung der Mondentfernung wird in fünf Etappen erarbeitet und angewendet. Bearbeitung und Auswertung einer Mondfotografie werden hier durch ein Beispiel veranschaulicht.
Heranführung der Lernenden an das Thema
Überblick
Da die Bestimmung des Mondabstandes mithilfe einer Mondfinsternis auf komplexen geometrischen und mathematischen Zusammenhängen basiert, werden die Lernenden schrittweise an das Thema herangeführt. Die folgende Gliederung hat sich dabei bewährt:1. Mondfinsternisse
Allgemeine Informationen: Wie kommen Mondfinsternisse zustande?2. Der Winkelradius der Sonne
Was ist ein Winkelradius? Wie kann man ihn messen? Welche Aussagen lassen sich daraus über den Kernschatten der Erde gewinnen?3. Der Winkelradius des Mondes
Wie kann man den Winkelradius des Mondes messen? Weshalb funktionieren die Methoden zur Messung des Winkelradius der Sonne (Schritt 2) hier nicht?4. Winkelradius des Kern-Erdschattens in Mondentfernung
Was versteht man darunter? Wie kann man ihn mithilfe einer Mondfinsternis bestimmen?
5. Berechnung des Mondabstandes
Die bisherigen Erkenntnisse werden zusammengeführt und die Mondentfernung mithilfe der bei einer Finsternis aufgenommenen Fotos berechnet.
Ausführliche Darstellung der Theorie
- mondabstand_mondfinsternis.pdf
Die mathematischen Zusammenhänge werden in dem Dokument mit der Herleitung der verwendeten Formeln sowie mithilfe entsprechender Grafiken ausführlich dargestellt.
VorschauIm Classroom-Manager speichern - mondabstand_mondfinsternis.odt
Informationen zu den mathematischen Zusammenhängen und ihrer Herleitung im OpenOffice-Format
Im Classroom-Manager speichern
Mondfotografie
Der Winkelradius des Erdschattens in Mondentfernung
Für die Bestimmung des Winkelradius (Schritt 4) ist die Auswertung eines Fotos von einer Mondfinsternis entscheidend. Der Kernschatten, der während der Finsternis auf dem Mond zu sehen ist, lässt sich mit dem Winkeldurchmesser des Mondes vergleichen.Der halb verfinsterte Mond wird fotografiert
Der gesamte Mond wird, während er etwa halb vom Kernschatten der Erde bedeckt ist, mit einer Vergrößerung beziehungsweise Auflösung fotografiert, die hoch genug ist, um Details der Finsternis erkennen zu können. Die Digitalkamera sollte über einen mindestens achtfachen optischen Zoom verfügen. Alternativ kann die Kamera auch an ein kleines Teleskop angeschlossen werden. Beim Fotografieren sollte auf jeden Fall ein Stativ verwendet werden. Abb. 1 (linke Teilabbildung) zeigt ein entsprechendes Ergebnis. Man sieht deutlich, dass sich der Kernschatten nicht scharf von dem Bereich des Halbschattens abgrenzt, sondern dass beide weich ineinander übergehen.Wenn man schon mal dabei ist …
Bei der Gelegenheit bietet es sich natürlich auch an, den gesamten Verlauf der Mondfinsternis fotografisch zu dokumentieren, im Idealfall vom Beginn bis zu Ende der Verfinsterung. Auch, wenn dies zum Zwecke der Entfernungsbestimmung nicht erforderlich ist (dafür reicht ein einziges Foto aus), kann man mit dem ohnehin verwendeten Bildbearbeitungsprogramm den Verlauf des Ereignisses in einer kleinen Kollage sehr schön darstellen.Bildbearbeitung am Rechner
Kontrastierung der Schattengrenze am Rechner
Um den Winkelradius des Kernschattens möglichst exakt bestimmen zu können, muss die Grenze zwischen Kern- und Halbschattenbereich durch eine Verstärkung des Kontrastes hervorgehoben werden. Die ist mit den gängigen Bildbearbeitungsprogrammen einfach durchzuführen. In dem hier vorgestellten Beispiel wurde die kostenfreie Open Source Software GIMP verwendet.- GIMP-Homepage
Informationen zur kostenfreien Bildbearbeitungssoftware und Downloadmöglichkeit
Bildbearbeitung mit GIMP
Öffnet man mit dem Programm die Mondfoto-Datei, lässt sich die Grenze des Kernschattens durch den Schwellwerte-Regler im Farben-Menü hervorheben (Abb.1, Mitte). Unter der Voraussetzung, dass der scharfe Rand des Mondes nicht mit weißen Pixeln durchsetzt sein darf, stellt man den Regler so niedrig wie möglich ein. Je nach Geschmack kann man über das Farben-Menü und die Funktion "Invertieren" den Mond schwarz und den Hintergrund weiß darstellen (Abb.1, rechts). In dem Ergebnis kann man nun gut erkennen, dass der Kernschatten, den die kugelförmige Erde auf den Mond wirft, auf der Mondoberfläche tatsächlich kreisförmig abgebildet wird. Die Kreisbogenform der Schattengrenze ist durch die nachträgliche Bearbeitung deutlich besser auszuwerten.Bestimmung von Kernschattenradius und Mondradius
Projektion oder Ausdruck des bearbeiteten Mondbildes
Das bearbeitete Bild kann nun vergrößert ausgedruckt oder auf eine Tafel projiziert werden. Ziel ist es, den auf der Tafel abgebildeten "Radius" des Mondes mit dem zu ermittelnden abgebildeten "Radius" des Kernschattens in Relation zu setzen - entweder auf Ausdrucken oder mithilfe des an die Tafel projizierten Bildes. Hieraus ergibt sich dann die Relation des Winkelradius des Mondes und des Kernschattens in Mondabstand, die sich im gleichen Verhältnis wie die Radien der Projektion teilen müssen.Geometrische Auswertung
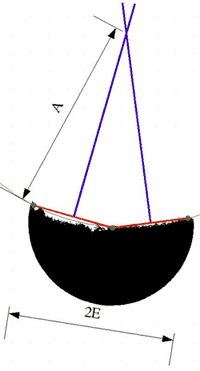
Abb. 2 veranschaulicht, wie man den Radius des Kernschattens bestimmt (A = Projektion des Kernschattenradius, E = Projektion des Mondradius). Die Konstruktion kann auch mit einem Vektorgrafikprogramm (zum Beispiel OpenOffice-Anwendung Draw) erzeugt werden. Zunächst wählt man drei Punkte, die auf dem Kreisbogen liegen (grün), und verbindet diese zu zwei Sekanten (rot). Anschließend werden die Mittelsenkrechten (blau) der Sekanten gebildet, die sich im Mittelpunkt des Kreises treffen. Damit ergibt sich der Radius A des abgebildeten Kernschattens durch den Abstand zwischen den grünen Punkten auf dem Kreisbogen und dem Schnittpunkt der blauen Mittelsenkrechten. Der Radius E des abgebildeten Mondes lässt sich über dessen leicht bestimmbaren Durchmesser berechnen. Aus Schritt 3 (siehe oben) ist der Winkelradius des Mondes epsilon bekannt. Gesucht ist der Winkelradius alpha des Kernschattens der Erde (in Mondentfernung). Wenn wir das Verhältnis alpha/epsilon kennen würden, könnten wir alpha direkt berechnen. Das Verhältnis alpha/epsilon ist nämlich genau so groß, wie das Verhältnis der Radien A/E auf dem Ausdruck (Abb. 2).Weiterlesen
- Methodische und fachliche Hinweise
Wodurch zeichnen sich die Mondfinsternis- und die Triangulationsmethode zur Entfernungsbestimmung aus? Wie messen Forscher die Entfernung zum Mond?